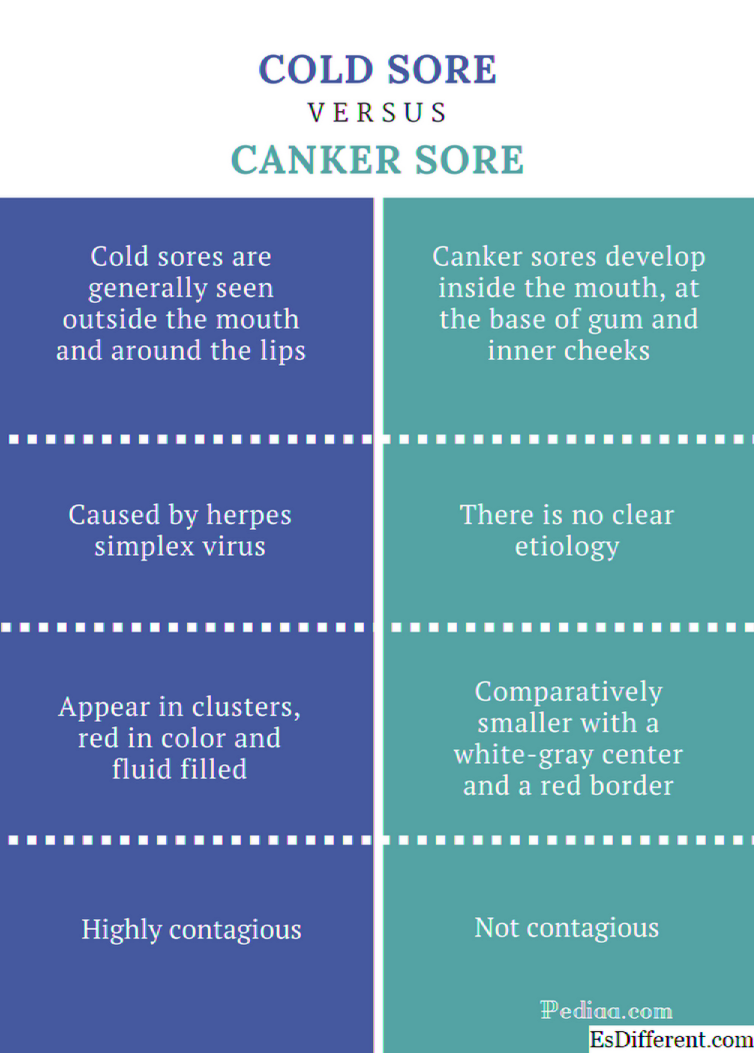
Точечный продукт и кросс-продукт

Dot Product vs Cross Product

Точечный продукт и кросс-продукт имеют несколько применений в физике, технике и математике. Перекрестное произведение, известное как векторное произведение, является двоичной операцией на двух векторах в трехмерном пространстве. Перекрестное произведение приводит к вектору, который перпендикулярен как векторам, которые умножаются, так и нормальны к равнине.

В алгебраических операциях точечный продукт принимает две последовательности с одинаковой длиной чисел и дает одно число. Он получается путем умножения соответствующих записей и последующего суммирования продуктов.

Если векторы называются «a» и «b», то точечный продукт представлен «a. б. «Это равно величинам, умноженным на косинус углов. В векторах «a» и «b» поперечное произведение представлено «a X b». Это равно величинам, умноженным на синус углов и затем умноженным на «n» единичный вектор.

Можно заметить, что величина точечного произведения является максимальной, тогда как в кросс-произведении она равна нулю. Точечный продукт и кросс-продукт полагаются на метрику евклидова пространства. Однако перекрестный продукт также зависит от ориентации выбора.

Точечный продукт обычно используется, когда требуется проецировать вектор на другой вектор. Некоторые примеры точечных продуктов:

Вычисление расстояния точки до плоскости. Вычисление расстояния точки до линии. Вычисление проекции точки.

Перекрестный продукт имеет множество применений, таких как:

Вычисление расстояния точки до плоскости. Вычисление зеркального света.

Резюме:

1. Кросс-произведение или векторный продукт представляет собой двоичную операцию на двух векторах в трехмерном пространстве. 2. В алгебраических операциях произведение точек принимает две последовательности с одинаковой длиной чисел и дает одно число. 3. Перекрестное произведение приводит к вектору, перпендикулярному как векторам, которые умножаются, так и нормальны к плоскости. 4. Точечный продукт получается путем умножения соответствующих записей и суммирования произведений. 5. Величина точечного произведения является максимальной, тогда как в кросс-продукте она равна нулю. 6. Точечный продукт обычно используется, когда необходимо проецировать вектор на другой вектор. 7. Если векторы называются «a» и «b», то точечный продукт представлен «a. b. «В векторах« a »и« b »поперечное произведение представлено« a X b ».